「そろばん」で面心立方格子の充填率を計算する？

大学受験で登場する化学の問題に「そろばんで」挑戦してみます。

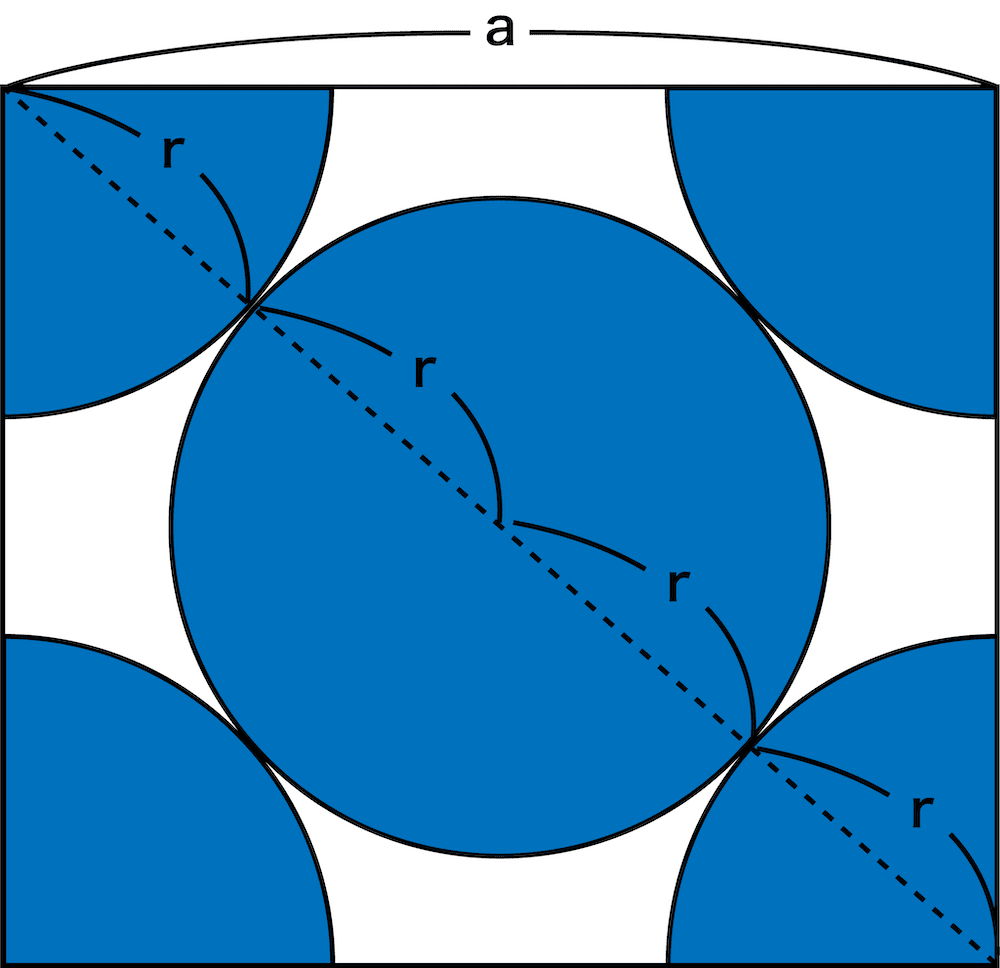
面心立方格子の単位格子の体積に占める原子（球）の個数は「４」個になります。

この球の半径rは格子1辺の長さaを用いて以下の通りです。

a = 4√2r

この半径 r の球４個分の体積は

√2 / 6 π a³

となり、単位格子の体積が a の3乗なので、充填率は以下の式で求まります。

√2 / 6 π

となります。ここで、さすがに π は3.14として√2は珠算式暗算で≒1.414と出せます。

この結果、充填率は0.74 → 74% ということが分かります。

アンダーラインが珠算式暗算の威力を発揮できるところです。